Kelsey Houston-Edwards in Quanta:
At first, topology can seem like an unusually imprecise branch of mathematics. It’s the study of squishy play-dough shapes capable of bending, stretching and compressing without limit. But topologists do have some restrictions: They cannot create or destroy holes within shapes. (It’s an old joke that topologists can’t tell the difference between a coffee mug and a doughnut, since they both have one hole.) While this might seem like a far cry from the rigors of algebra, a powerful idea called homology helps mathematicians connect these two worlds.
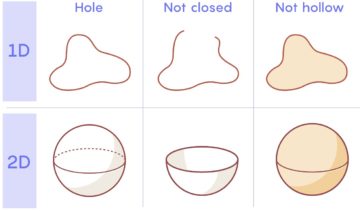
The word “hole” has many meanings in everyday speech — bubbles, rubber bands and bowls all have different kinds of holes. Mathematicians are interested in detecting a specific type of hole, which can be described as a closed and hollow space. A one-dimensional hole looks like a rubber band. The squiggly line that forms a rubber band is closed (unlike a loose piece of string) and hollow (unlike the perimeter of a penny).
Extending this logic, a two-dimensional hole looks like a hollow ball. The kinds of holes mathematicians are looking for — closed and hollow — are found in basketballs, but not bowls or bowling balls.
But mathematics traffics in rigor, and while thinking about holes this way may help point our intuition toward rubber bands and basketballs, it isn’t precise enough to qualify as a mathematical definition.
More here.