Ken Wessen in Plus Magazine:
As computers are constantly becoming faster and better, many computational problems that were previously out of reach have now become accessible. But is this trend going to continue forever, or are there problems computers will never, ever be able to solve? Let's start our consideration of this question by looking at how computer scientists measure and classify the complexity of computational algorithms.
Suppose you are responsible for retrieving files from a large filing system. If the files are all indexed and labelled with tabs, the task of retrieving any specific file is quite easy — given the required index, simply select the file with that index on its tab. Retrieving file 7, say, is no more difficult than retrieving file 77: a quick visual scan reveals the location of the file and one physical move delivers it into your hands. The total number of files doesn't make much difference. The process can be carried out in what is called constant time: the time it takes to complete it does not vary with the number of files there are in total. In computers, arrays and hash-tables are commonly used data structures that support this kind of constant time access.
Now suppose that over time the tabs have all fallen off the files. They are still indexed and in order, but you can no longer immediately spot the file you want. This introduces the requirement to search, and a particularly efficient way to do so is a binary search. This involves finding the middle file and seeing whether the file you need comes before or after. For example, when looking for file 77, pull out the middle file and see if its index is smaller or larger than 77, and then keep looking to the left or right of the middle file as appropriate.
With this single step you have effectively halved the size of the problem, and all you need to do is repeat the process on each appropriate subset of files until the required file is found. Since the search space is halved each step, dealing with twice as many files only requires one additional step.
Writing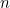 
for the total number of files, it turns out that as 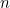grows, the number of steps it takes to solve the problem (that is, the number of steps it takes to find your file) grows in proportion to 
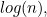the logarithm to base 
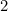of 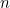(see the box below to find out why). We therefore say that a binary search is logarithmic, or, alternatively, that it has computational complexity 
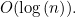This is the so-called big O notation: the expression in the brackets after the O describes the type of growth you see in the number of steps needed to solve the problem as the problem size grows (see the box on the left for a formal definition).
A logarithmic time process is more computationally demanding that a constant time process, but still very efficient.
But what if over time the loss of the tabs has allowed the files to become disordered? If you now pull out file 50 you have no idea whether file 77 comes before or after it.
More here.