What follows is an essay adapted from a talk, delivered in 2010 to teenagers and parents in my hometown of Cupertino, California. The talk concerned the surfaces of things, like bodies and planets, and abstract surfaces, like the Möbius strip and the torus. The goal was to learn about the world by studying surfaces mathematically, to learn about mathematics by studying the way we study surfaces, and, ideally, to learn about ourselves by studying how we do mathematics.
Joshua Batson in Hypocrite Reader:
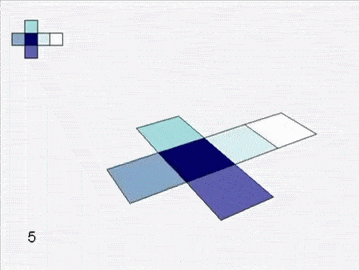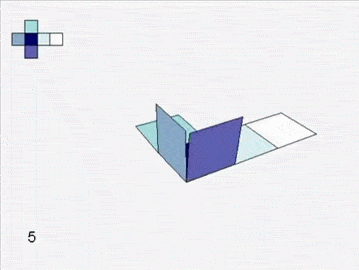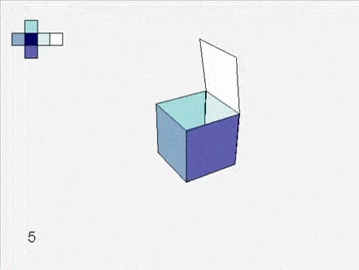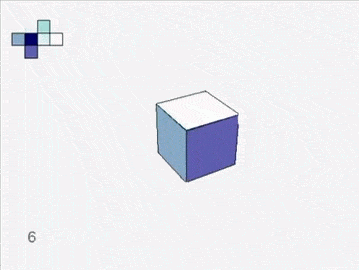
An atlas of squares assembles into a cube.
Imagine that you are an emperor regarding a great expanse from a tall peak. Though your territory extends beyond your sight, a map of the entire empire hangs on the wall in your study, seventy interlocking cantons. On your desk lies a thick, bound atlas. Each page is a detailed map of a county whose image on the great map is smaller than a coin.
You dream of an atlas of the world in which the map of your empire would fill but a single page. You send forth a fleet of cartographers. They scatter from the capitol and each, after traveling her assigned distance, will make a detailed map of her surroundings, note the names of her colleagues in each adjacent plot, and return.
If the world is infinite, some surveyors will return with bad news: they were the member of their band to travel the furthest and uncharted territory lies on one side of their map. But if the world is finite, there will be many happy surprises: a friend last seen in the capitol is rediscovered thousands of miles from home, having taken another path to the same place. Their maps form an atlas of the world.
You have another dream, in which the whole world is contained in your capable hands, miniature and alive. Upon waking, you begin to tear the pages out of the atlas and piece them together, using the labels on the edge of each page to stitch it to its neighbors, constructing ever larger swaths of territory.
Soon you are left with six grand charts. You fit them together and they lift off the table to form a cube.
More here.
